如果在銀行內存入100元且利率為1%,則一年之後得到1元的利息,然而第二年的利息,由於將第一年的利息1元納入計息本金中,因此為1.01元而非1元,這個過程又稱為複利計算。複利可以考慮到任何一分錢的時間價值但是卻可能對數學不好或是手上沒有計算機的投資人帶來計算上的困難。因此數學家發明了72法則,提供投資人一個簡易的計算方式,以下將會介紹72法則推倒及應用。
什麼是72法則?
72法則又稱為複利72法則,最初是假設以1%報酬複利計算,經過72年後,本金就會翻成1倍,簡單說就是(1+1%)的72次方大約就等於是2。72法則根本上是一個簡單快速計算複利的公式,雖然不能百分百準確但是可以幫助投資者在短時間內算出一筆投資的年化收益率或是回本時間。
72法則的歷史由來?
72法則由一位義大利數學家也被稱為會計之父的盧卡·帕喬利(Luca Pacioli)在其1494年的著作《算術、幾何、比例總論》中所提出,將在以下段落介紹72法則的推導。
72法則的運作原理和公式?
以下為簡化的72法則原理的推導:
- (1 + r )^n = 2:(1+年化收益率)的n年次方我們希望發翻倍,所以等式右邊為2
- 對等式兩邊同時取ln (就像是我們之前國中數學學的取log只是將底數的10換成 Exponential):ln((1+r) ^n) = ln (2) = n × ln(1+r) = 0.693
- 因為r是一個極小的數值,因此ln(1+r)會近似於r,所以後續推導由r代替ln(1+r):n × r = 0.693 = 69.3%
- 以上的算式基本上就是72法則的原型,最初的推倒結果為69.3%,但是經過數學家調整最終採用72%,除了計算方便外,報酬率10%以上時,使用72的計算誤差更小。
計算本金翻倍時間:72 ÷ 年化報酬率 = 本金翻倍時間
計算報酬率:72 ÷ 本金翻倍時間 = 本金翻倍時間
我們可以簡單舉的例子:根據統計,0056 目前年化報酬率為7.46%,那0056的本金翻倍時間即是72 ÷ 7.46 = 9.65年。目前股價為25.66元,假設我們現在買入一張投入成本25,660元,那9.65年之後投資者(加上原先本金就會收回月51,000元,即25,660 * ( 1+7.46%)的9.65次方。
換一個角度看,如果一筆投資,我們希望可以在10年回本,那我們需要的年化投資收益率就要在7.2%左右,即(1+7.2%)的10次方大約為2。
該法則不論是最初推倒的69.3%還是72%在收益率較小時都相對精準,根據計算在8%左右算出來的結果是最為精確的,但一旦報酬率越高,簡易的計算變化失真。
72法則圖表和Excel模板?
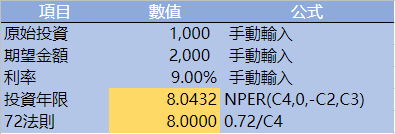
使用72法則計算投資年限後同樣可以透過excel模板進行檢查以及比較,手動輸入投入、預期收回金額以及利率後,使用NPER公式同樣可以計算出投資年限 [ NPER (利率, 期間收益(例如股利等), 期初投資(記得加上負號表示資金流出), 收回金額)] 可以透過公式以及直接計算來比較可以發現基本差異不大。
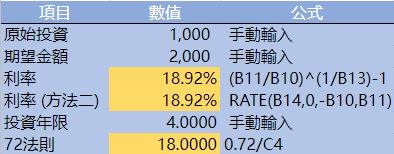
計算收益率也是同理,手動輸入投入、預期收回金額以及投資年限後,不論是直接逆算,或是使用RATE公式都可以進行驗證 [RATE (投資年限, 期間收益(例如股利等), 期初投資(記得加上負號表示資金流出), 收回金額)],可以發現由於該收益率已經超過10% ,72法則結果略有失準約1%,但大致結果仍為相似。
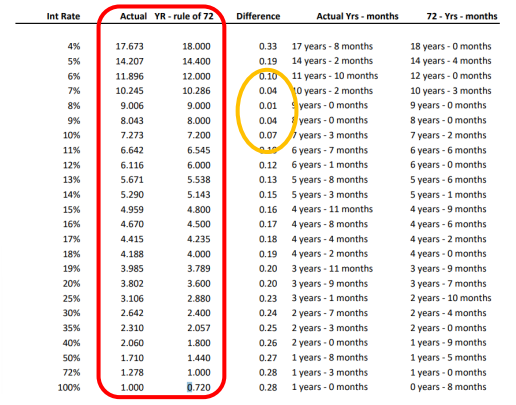
以上為經計算之不同利率下,實際投資年限對比72法則結果,紅框為投資年限比較,如果是尚未法理解excel計算邏輯的讀者可以參考以上該表並了差異並思考該差異是否會對投資造成重大影響。有可以透過該表格發現最準確的範圍大約在利率6% – 10%左右(黃框部分)。
如何使用72法則?
在介紹72法則的原理以及公式時已為讀者舉了兩個投資計算應用的例子,但其實72法則除了可以運用在投資收益的計算上也可以用來計算任何關於複合收益率與成長率的事物,例如通貨膨脹的計算,GDP的成長等。例如:之前日本的人口增長率大約為 0.2 %,如果我們想要計算日本人口何時會增長到目前的一倍,我們同樣可以使用72 ÷ 0.2 = 360年。
但是使用72法則有意下幾點需要注意:
- 該法則只是用在複利計算上,如果是單利投資則不適用
- 該法則並非完全準確,如同前段所述最準確的範圍大約在6% – 10%左右,而且如果投資總金額較高,每個增減一個百分點對於整體收益金額的影響就會相當顯著所以需要注意。
- 由於設計的基礎是建立在要將投資金額翻倍,所以在面對負利率的情況下未必適用。
後續,也有許多人提出衍生的計算法則例如:70法則,這是建立在連續利的情況下針對 (er)^n = 2 進行指對數處理,同樣獲得69.3%左右的數值,最終取70計算。但是由於連續複利在投資上較少見所以大部份投資人來是會採取最初的72法則。
結語
整而言之,72法則是一個相當實用的計算方式,能幫助投資人快速判斷投資的收益率或是應有的投資年限,加上一般台灣國內投資較少有年化收益率極大超過10%的案例,偏差結果大部分尚可忽略,因此適用度高。不過也要再次重申,簡便算法與實際計算的差異對於大額投資可能造成的影響甚著,因此需要審慎用之。